Game 6
What if arrivals are in batches?
Click "start" on the above to begin.
An introduction and review of the game is given below.
An introduction and review of the game is given below.
In this game we will build on the impact and learning from the previous games and add another feature into the process.
To-date we have discovered the impact of dependent events and statistical fluctuations and we've looked at the environment where the statistical fluctuations vary at each stage of the process, and where there is always one weakest link in the chain. We have also looked at how buffering this weakest link can improve the overall performance of the system.
Throughout previous games the arrival pattern has been based upon the throw of the first step in the process. In this game we're going to look at a number of different arrival patterns and see what impact they have on the performance of the system.
The arrival pattern is set by clicking on the set arrival pattern button. You will be presented with a number of possible patterns, for example, the first one is random where throughout the 20 throws there will be one batch of 10.
As with the previous game you can also select a buffer level. As you go through the 20 throws you can adjust the buffer level to see how this impacts throughput and to see how best to cope with the different arrival patterns.
Try different arrival patterns and try with the weakest link at various steps in the process - towards the beginning, towards the middle, towards the end - and try setting different buffer levels and see what impact this has on throughput, the number of people in the system and the time in the system.
To-date we have discovered the impact of dependent events and statistical fluctuations and we've looked at the environment where the statistical fluctuations vary at each stage of the process, and where there is always one weakest link in the chain. We have also looked at how buffering this weakest link can improve the overall performance of the system.
Throughout previous games the arrival pattern has been based upon the throw of the first step in the process. In this game we're going to look at a number of different arrival patterns and see what impact they have on the performance of the system.
The arrival pattern is set by clicking on the set arrival pattern button. You will be presented with a number of possible patterns, for example, the first one is random where throughout the 20 throws there will be one batch of 10.
As with the previous game you can also select a buffer level. As you go through the 20 throws you can adjust the buffer level to see how this impacts throughput and to see how best to cope with the different arrival patterns.
Try different arrival patterns and try with the weakest link at various steps in the process - towards the beginning, towards the middle, towards the end - and try setting different buffer levels and see what impact this has on throughput, the number of people in the system and the time in the system.
Game 6 behaviour and analysis
In this game the slowest step is buffered to protect it but it no longer sets the pace for entry into the system. In this respect it is much closer to real health and social care systems where external sources determine the supply. Further, the arrivals may be batched, which again more closely simulates how new people enter the system. Again, there are many possible variations of this game and we will present a few general observations.
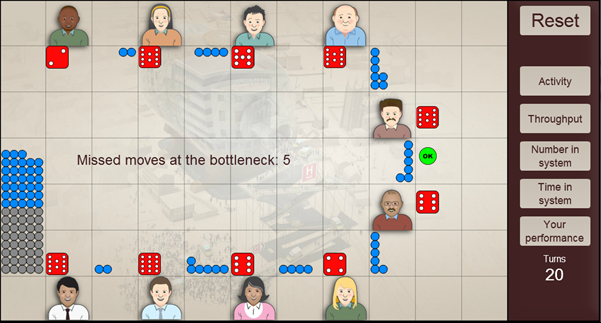
For the case where batching is infrequent, i.e. the general arrival is dominated by random values with a few batches of slightly above average number, it is reasonable to expect the buffer to have a fairly constant flow of new people. In this case the buffer can be set relatively low. In the example below the arrival pattern is random with at least one batch of 10, and has an initial buffer value of 8. The number of missed moves at the bottleneck is 5.
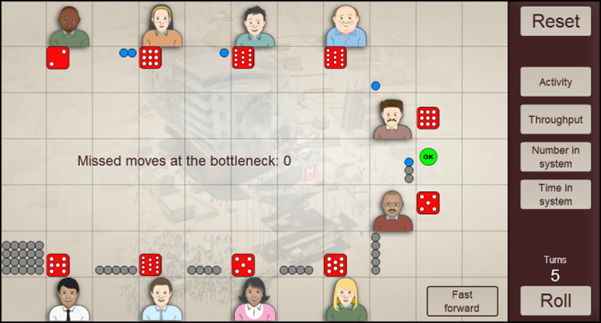
Now consider the same system but with a much more batch-oriented arrival pattern; 8 low number of arrivals followed by one large. In this situation you initially run the risk of the buffer having too few people so that there is missed service opportunity.
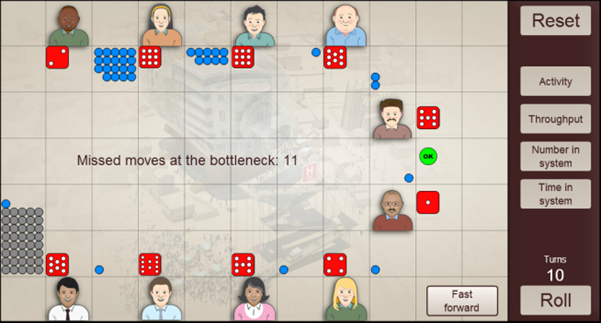However, after this, the number of people in the system increases and significant queues may form at various stages as the influx is distributed through the system.
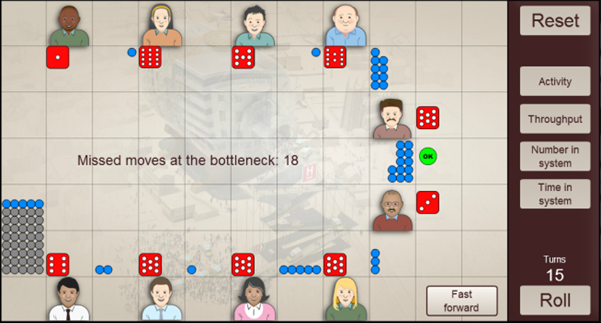
This will replenish the buffer; however, the subsequent low number of arrivals may again mean the buffer empties between batches if the initial level is not sufficient. In such cases it may be desirable to increase the buffer size.
As with the previous game, there is a large scope for variability in outcomes depending not only on the arrival pattern but also on the variability and capacities of each step, and the location of the slowest step in the system. All of these have an impact on the optimal buffer size.
For the case where batching is infrequent, i.e. the general arrival is dominated by random values with a few batches of slightly above average number, it is reasonable to expect the buffer to have a fairly constant flow of new people. In this case the buffer can be set relatively low. In the example below the arrival pattern is random with at least one batch of 10, and has an initial buffer value of 8. The number of missed moves at the bottleneck is 5.
Now consider the same system but with a much more batch-oriented arrival pattern; 8 low number of arrivals followed by one large. In this situation you initially run the risk of the buffer having too few people so that there is missed service opportunity.
However, after this, the number of people in the system increases and significant queues may form at various stages as the influx is distributed through the system.
This will replenish the buffer; however, the subsequent low number of arrivals may again mean the buffer empties between batches if the initial level is not sufficient. In such cases it may be desirable to increase the buffer size.
As with the previous game, there is a large scope for variability in outcomes depending not only on the arrival pattern but also on the variability and capacities of each step, and the location of the slowest step in the system. All of these have an impact on the optimal buffer size.