Game 5
The "drum, buffer, rope" approach to control
Click "start" on the above to begin.
An introduction and review of the game is given below.
An introduction and review of the game is given below.
In this game we explore the impact of both dependent events and statistical fluctuations at the same time.
The dependent events are as in previous games - we have 10 work stations. However, in this instance the statistical fluctuations we see are not as in the previous games - the amount of variation is considerable at each step. So not only do we have different variation at each step, we also have different averages at each step. So, in essence, there is bound to be a weakest link in the system - there is bound to be one step with a lower performance than everywhere else.
To facilitate the learning, we have the ability here to change the level of variation of each and every step of the system. You can select any step and change the lowest and highest throw, and it will give the average for that particular work station. (Note, the game below changes the highest and lowest rolls using a slider input rather than typed inputs.)
So, in this game, we see very high levels of variation mixed with different average variation at each and every step. However, when you have finished setting the various stages you will also notice there is one step which is our weakest link, or our slowest step in the process. At this stage we can introduce the concept of buffer management where, if you click the set buffer level, you can select the initial buffer level that you want to place in front of that weakest link. It is suggested that you start with 12 counters. When you press the start button the game will set up as before but your 12 counters will appear just before the weakest link.
You will notice that the colour of the buffer in front of the weakest link will change from green to amber to red. In essence we're seeing how much protection we have of this weakest link. If you see there is not sufficient protection then you can click the change buffer and increase the buffer by the selected amount by selecting the amount of extra people you wish to be at that step in the system. This extra amount of people will be introduced into the front end of the system. Equally, you may want to click to reduce the buffer. In which case, you can slow down the release of new people into the system.
The purpose of the game is to understand how the weakest link impacts the perfomrance of the system as a whole. What you will see is that as the game progresses the size of the buffer is important as it soaks up the variation in other parts of the system.
The dependent events are as in previous games - we have 10 work stations. However, in this instance the statistical fluctuations we see are not as in the previous games - the amount of variation is considerable at each step. So not only do we have different variation at each step, we also have different averages at each step. So, in essence, there is bound to be a weakest link in the system - there is bound to be one step with a lower performance than everywhere else.
To facilitate the learning, we have the ability here to change the level of variation of each and every step of the system. You can select any step and change the lowest and highest throw, and it will give the average for that particular work station. (Note, the game below changes the highest and lowest rolls using a slider input rather than typed inputs.)
So, in this game, we see very high levels of variation mixed with different average variation at each and every step. However, when you have finished setting the various stages you will also notice there is one step which is our weakest link, or our slowest step in the process. At this stage we can introduce the concept of buffer management where, if you click the set buffer level, you can select the initial buffer level that you want to place in front of that weakest link. It is suggested that you start with 12 counters. When you press the start button the game will set up as before but your 12 counters will appear just before the weakest link.
You will notice that the colour of the buffer in front of the weakest link will change from green to amber to red. In essence we're seeing how much protection we have of this weakest link. If you see there is not sufficient protection then you can click the change buffer and increase the buffer by the selected amount by selecting the amount of extra people you wish to be at that step in the system. This extra amount of people will be introduced into the front end of the system. Equally, you may want to click to reduce the buffer. In which case, you can slow down the release of new people into the system.
The purpose of the game is to understand how the weakest link impacts the perfomrance of the system as a whole. What you will see is that as the game progresses the size of the buffer is important as it soaks up the variation in other parts of the system.
Game 5 behaviour and analysis
This version of the game introduces many possible variations for the player to investigate. We will start by observing how buffer management through use of the drum, buffer, rope (DBR) control method affects the flow.
The weakest link for the game below is station 6 and so we will let it control the flow of people into the system.
As you play the game you will notice that the deliberate use of a queue or buffer of people in front of the slowest step means that it nearly always has a sufficient number of people waiting to be treated, so the probability of rolling a die value that is higher than the people in the buffer is low.
You will also notice that if the slowest step rolls a succession of low values, the buffer level may increase to a relatively high value. However, when this station treats a low number of people in a round, the number of new people introduced into the system is also low. As this feeds through, it ensures that the buffer does not become overly large.
A third observation is that, because the flow into the system before the buffer and the flow after the buffer is all controlled by the slowest step, all other the other stations usually have sufficient capacity to service their own queues. In other words, queues are unlikely to grow to unmanageable or significant sizes in other parts of the system.
Moving the position of the slowest step can affect what buffer level is required to minimise the probability that the queue length is shorter than the capacity of that step in a round. For example, consider the case where the second station is slowest step.
As this step controls the input into the system, then whatever passes from station 2 to station 3 will be exactly replenished by an equal number of new arrivals from station 1 to station 2. Given that station 2 can only treat a maximum of 6 people in any round, then imposing a buffer level of 6 is sufficient to ensure that all the available capacity of station 2 will always be used. This is in contrast to the game state below where the slowest step is once again station 6.
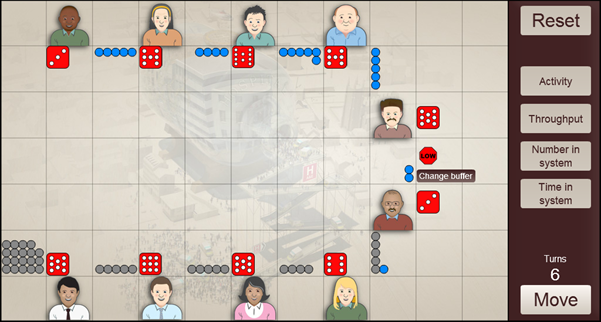In this situation a buffer level of 6 was specified, however, as there is still some random variation in throughput upstream, this initial level is seen to be too low to always ensure that the slowest step always has enough people to work with, so in round 6 the slowest step has rolled a 3 and only has 2 people in the queue. Increasing the initial buffer size can mitigate this.
In general, as the potential for variability, and the delay for controlled feed into the system reaching the buffer increases, as occurs when the slowest step is nearer the end of the chain of services, it may be necessary to impose a higher desired buffer value for such cases. However, the details do depend on the specific variability and the average capacity of steps preceding the slowest step.
These effects also come into play when a manual intervention is made to increase or reduce the buffer. This might be done when you perceive there to be a possibility of the buffer running low or being too high. The intervention controls new entry into the system. However, there is a delay to its effect on the number in the buffer as the effect of the intervention has to travel through all the preceding steps first. So, in the example game shown above, you might want to boost the buffer by introducing more people into the system. However, any increase in new introductions will take at least 5 rounds to reach the buffer. Similarly, in the game below, you might want to reduce the number in the buffer by reducing the number of new people introduced into the system. Again, any reductions will take at least five rounds to reach and affect the buffer.
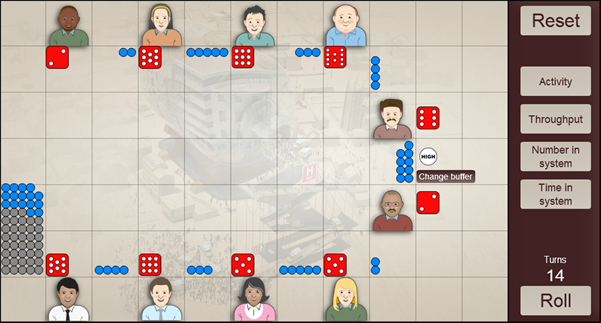So the time lag between action and effect depends on how far away the buffer is from the start of the chain of services. Again, you can control whether warnings are issued at high or low buffer values by setting the desired buffer level.
As you play the game you will notice that the deliberate use of a queue or buffer of people in front of the slowest step means that it nearly always has a sufficient number of people waiting to be treated, so the probability of rolling a die value that is higher than the people in the buffer is low.
You will also notice that if the slowest step rolls a succession of low values, the buffer level may increase to a relatively high value. However, when this station treats a low number of people in a round, the number of new people introduced into the system is also low. As this feeds through, it ensures that the buffer does not become overly large.
A third observation is that, because the flow into the system before the buffer and the flow after the buffer is all controlled by the slowest step, all other the other stations usually have sufficient capacity to service their own queues. In other words, queues are unlikely to grow to unmanageable or significant sizes in other parts of the system.
Moving the position of the slowest step can affect what buffer level is required to minimise the probability that the queue length is shorter than the capacity of that step in a round. For example, consider the case where the second station is slowest step.
As this step controls the input into the system, then whatever passes from station 2 to station 3 will be exactly replenished by an equal number of new arrivals from station 1 to station 2. Given that station 2 can only treat a maximum of 6 people in any round, then imposing a buffer level of 6 is sufficient to ensure that all the available capacity of station 2 will always be used. This is in contrast to the game state below where the slowest step is once again station 6.
In this situation a buffer level of 6 was specified, however, as there is still some random variation in throughput upstream, this initial level is seen to be too low to always ensure that the slowest step always has enough people to work with, so in round 6 the slowest step has rolled a 3 and only has 2 people in the queue. Increasing the initial buffer size can mitigate this.
In general, as the potential for variability, and the delay for controlled feed into the system reaching the buffer increases, as occurs when the slowest step is nearer the end of the chain of services, it may be necessary to impose a higher desired buffer value for such cases. However, the details do depend on the specific variability and the average capacity of steps preceding the slowest step.
These effects also come into play when a manual intervention is made to increase or reduce the buffer. This might be done when you perceive there to be a possibility of the buffer running low or being too high. The intervention controls new entry into the system. However, there is a delay to its effect on the number in the buffer as the effect of the intervention has to travel through all the preceding steps first. So, in the example game shown above, you might want to boost the buffer by introducing more people into the system. However, any increase in new introductions will take at least 5 rounds to reach the buffer. Similarly, in the game below, you might want to reduce the number in the buffer by reducing the number of new people introduced into the system. Again, any reductions will take at least five rounds to reach and affect the buffer.
So the time lag between action and effect depends on how far away the buffer is from the start of the chain of services. Again, you can control whether warnings are issued at high or low buffer values by setting the desired buffer level.