Game 1
A system of dependent events with statistical fluctuations
Click "start" on the above to begin.
An introduction and review of the game is given below.
An introduction and review of the game is given below.
In this first dice game we can explore the impact of a system of dependent events with statistical fluctuations.
Ten resources show the flow in a clockwise direction from the top left through to the bottom left, as shown in the figure below. Each resource has a single, six-sided die that will be used to indicate the number of people they can process on each throw. When you click on Start, four people will be allocated to a queue between each resource. When you then click Roll, all ten resources will roll their die and this will indicate their capacity for that particular throw. When you click Move, the people waiting in the queue will be processed through the resource and move onto the next station.
There is only one simple rule: the resource can only process people that were already waiting in the queue from the previous day; they are not able to process the people from the same day’s output of the previous workstation. In essence, this means the resources pass before they receive the output from the previous work station.
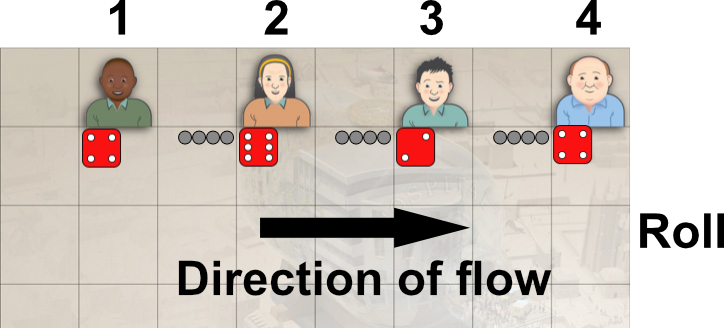The figure above shows the first four stations and their rolls.
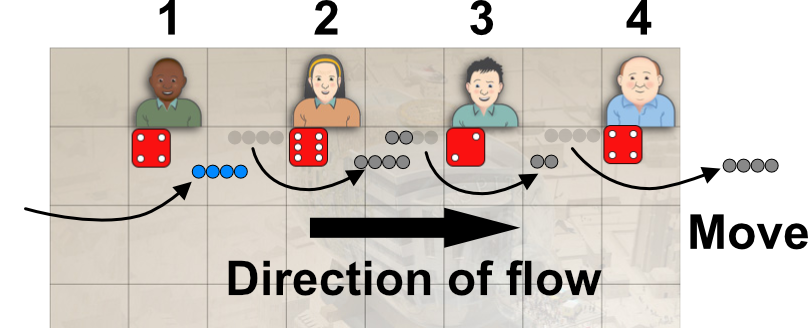The situation after the move round is as shown below.
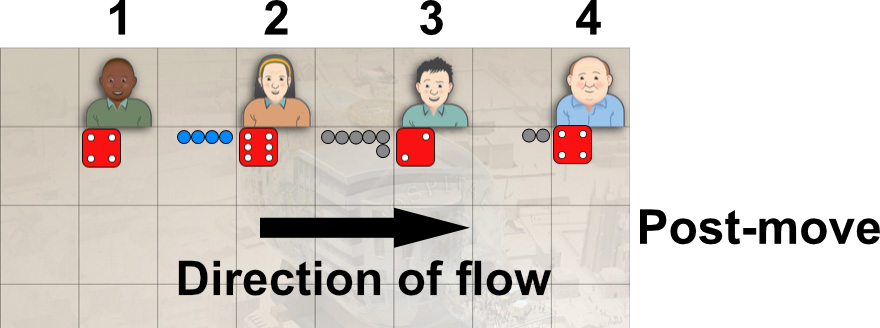As you continue to roll and move people through the system, you will notice the size of the queue between each work station may vary. It is interesting to explore how this changes over time. You can also keep an eye on the number of people in the system by click on the Number In System button and once people have gone through all ten resources you can also identify the time it took for people to pass through the whole system and the throughput of the system. New people entering the system are blue in colour to help you identify the flow over time. You will notice people are processed in a strict sequence of arrival.
After twenty rolls of the dice a new button ‘Your performance’ appears and you can examine your performance relative to a very large sample of others.
My suggestion is, you run the game a couple of times and notice the behaviours of the system and start to answer the following questions:
Ten resources show the flow in a clockwise direction from the top left through to the bottom left, as shown in the figure below. Each resource has a single, six-sided die that will be used to indicate the number of people they can process on each throw. When you click on Start, four people will be allocated to a queue between each resource. When you then click Roll, all ten resources will roll their die and this will indicate their capacity for that particular throw. When you click Move, the people waiting in the queue will be processed through the resource and move onto the next station.
There is only one simple rule: the resource can only process people that were already waiting in the queue from the previous day; they are not able to process the people from the same day’s output of the previous workstation. In essence, this means the resources pass before they receive the output from the previous work station.
The figure above shows the first four stations and their rolls.
- Player 1 rolls a four and will introduce four people into the system (blue).
- Player 2 rolls a six but only has four people to process. They cannot wait for the four new arrivals so she can only move the four people she has.
- Player 3 rolls a two and can only process two people, leaving two behind.
- Player 4 rolls a four and moves his four people.
The situation after the move round is as shown below.
As you continue to roll and move people through the system, you will notice the size of the queue between each work station may vary. It is interesting to explore how this changes over time. You can also keep an eye on the number of people in the system by click on the Number In System button and once people have gone through all ten resources you can also identify the time it took for people to pass through the whole system and the throughput of the system. New people entering the system are blue in colour to help you identify the flow over time. You will notice people are processed in a strict sequence of arrival.
After twenty rolls of the dice a new button ‘Your performance’ appears and you can examine your performance relative to a very large sample of others.
My suggestion is, you run the game a couple of times and notice the behaviours of the system and start to answer the following questions:
- Is the throughput, after twenty throws, as expected?
- Are any changes in work in progress as expected?
- What strategies might we adopt to try and improve the system?
Game 1 behaviour and analysis
The initial configuration of the system is 10 stations with 4 people between each station, giving a starting point of 36 people as work in progress.
The number of people processed through each station during a round is determined by the roll of a six-sided die. The average roll value of such a die is 3.5, so naively, one might expect each station to process on average 3.5 people per round. This means that over 20 rounds, 70 people should have been processed and left the system.
In practice, what happens is that random variations in the rolls mean that some players roll a higher value than the number of people they have in their queue, while others roll lower a value than the number of people they have in their queue. Those that roll a higher value do not process to their full potential as they do not have the people available to work with. Those that roll lower values than the number of people waiting can produce temporary bottlenecks. Such bottlenecks not only mean that a queue builds behind that particular station, but they also choke off supply to the rest of the system, meaning that subsequent stations are even more likely not to process to their potential capacity.
The above effects can be clearly seen in the game snapshot below, where the player at station 6 has rolled a number of low values leading to a temporary bottleneck. All but one of the players after station 6 has rolled a higher value than the number of people waiting, leading to a potential capacity of these four stations of 5 + 1 + 5 + 4 = 15 being realised as an actual movement of 7 people. Had more people been processed by station 6, more people would have been available in stations 7 to 10 to move.
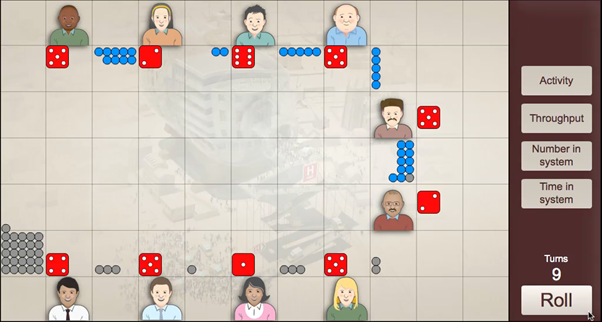The bottleneck may subside after only a few rounds, but to fully recover from it and clear the backlog, the bottleneck player and all those down-stream need to roll several consecutive high values. This is statistically less likely than a single player rolling a few low values, which is what caused the problem in the first place.
The temporary bottlenecks mean that although the average roll on each round is 3.5, the average number of people moved is significantly less than this. In fact, the most likely outcome of a game is that you get 53 through the system in 20 rounds; an average movement of 2.65 people per round, as shown in the diagram below.
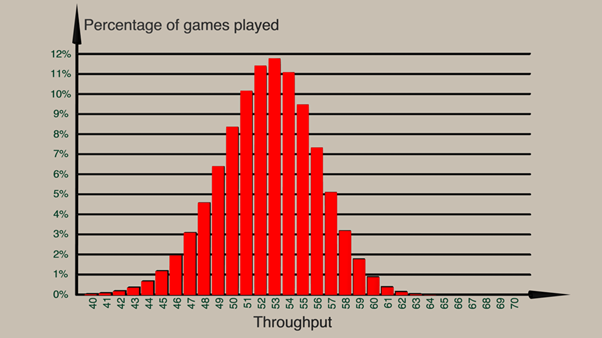An analysis of the results shows that about 99% of all games played will get between 44 and 62 people through the system. The above diagram also shows it is very unlikely that you will get 70 people through, although it is possible, but with odds that are around the order of magnitude of winning the UK National Lottery.
It should be noted that there is no restriction on people entering the system. This means that the roll value and movement value for the first station are equal, and will average 3.5. Because this is larger than the average number of people moved through all the subsequent stations, the number of people as work in progress in the system will gradually increase as the game progresses. Put simply – people enter the system faster than they leave it so the number in the system must grow.
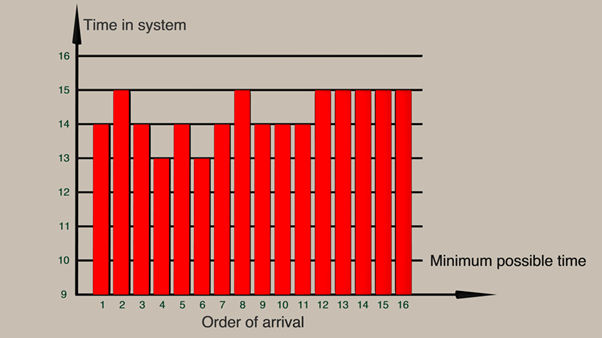
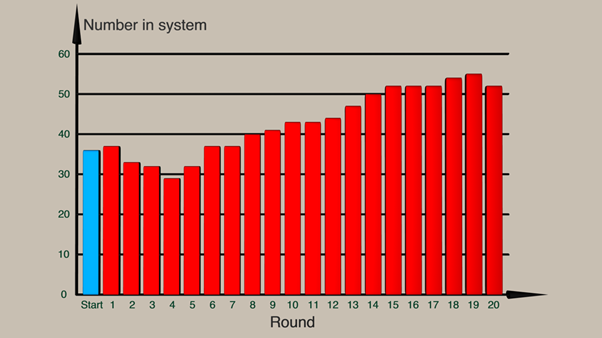Similarly, because queues start to grow as the work in progress grows and combined with the creation of temporary bottlenecks, the average passage time through the system also increases as the game progresses.
The number of people processed through each station during a round is determined by the roll of a six-sided die. The average roll value of such a die is 3.5, so naively, one might expect each station to process on average 3.5 people per round. This means that over 20 rounds, 70 people should have been processed and left the system.
In practice, what happens is that random variations in the rolls mean that some players roll a higher value than the number of people they have in their queue, while others roll lower a value than the number of people they have in their queue. Those that roll a higher value do not process to their full potential as they do not have the people available to work with. Those that roll lower values than the number of people waiting can produce temporary bottlenecks. Such bottlenecks not only mean that a queue builds behind that particular station, but they also choke off supply to the rest of the system, meaning that subsequent stations are even more likely not to process to their potential capacity.
The above effects can be clearly seen in the game snapshot below, where the player at station 6 has rolled a number of low values leading to a temporary bottleneck. All but one of the players after station 6 has rolled a higher value than the number of people waiting, leading to a potential capacity of these four stations of 5 + 1 + 5 + 4 = 15 being realised as an actual movement of 7 people. Had more people been processed by station 6, more people would have been available in stations 7 to 10 to move.
The bottleneck may subside after only a few rounds, but to fully recover from it and clear the backlog, the bottleneck player and all those down-stream need to roll several consecutive high values. This is statistically less likely than a single player rolling a few low values, which is what caused the problem in the first place.
The temporary bottlenecks mean that although the average roll on each round is 3.5, the average number of people moved is significantly less than this. In fact, the most likely outcome of a game is that you get 53 through the system in 20 rounds; an average movement of 2.65 people per round, as shown in the diagram below.
An analysis of the results shows that about 99% of all games played will get between 44 and 62 people through the system. The above diagram also shows it is very unlikely that you will get 70 people through, although it is possible, but with odds that are around the order of magnitude of winning the UK National Lottery.
It should be noted that there is no restriction on people entering the system. This means that the roll value and movement value for the first station are equal, and will average 3.5. Because this is larger than the average number of people moved through all the subsequent stations, the number of people as work in progress in the system will gradually increase as the game progresses. Put simply – people enter the system faster than they leave it so the number in the system must grow.
Similarly, because queues start to grow as the work in progress grows and combined with the creation of temporary bottlenecks, the average passage time through the system also increases as the game progresses.